- Attractive force which exists between anything that has a mass
- Inversely proportional to the distance between 2 interacting objects
- Directly proportional to the mass
- Mass = the amount of matter in an object
- Weight/force = the force applied on an object by gravity
Weight (Unit - Newton-N) = mass * gravity
Volume = how much space an object or substance takes up (cm3. M3. ml, l)
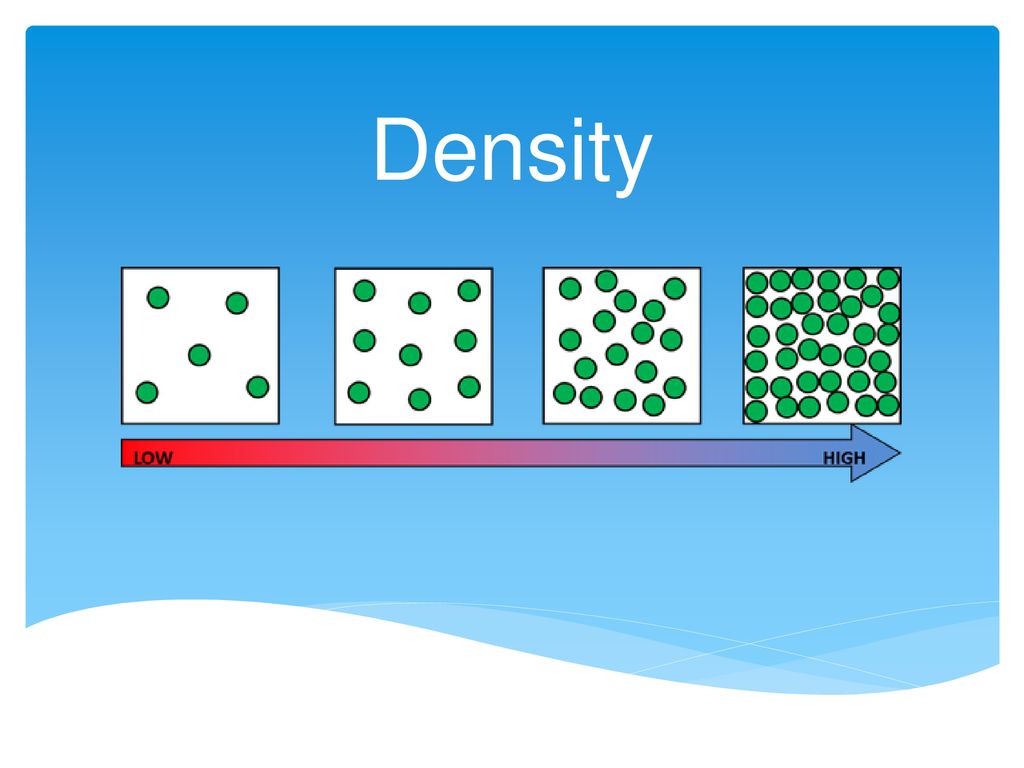
- Many masses stuffed into a little space of volume has more density.
- If masses are the same, density is inversely proportional to volume.
- If volumes are the same, density is directly proportional to mass.
Density = Mass/Volume
- Density tells us the mass of 1 cm3 of a material.
- Unit of density = g/cm3 (or) kg/cm3
To know the density of a material, measure its mass and volume.
Mass → measured using a balance
- There are different designs of balance (beam balance, spring balance, etc…)


(1) Regular shape: measure each side.
- Volume = length × width × height
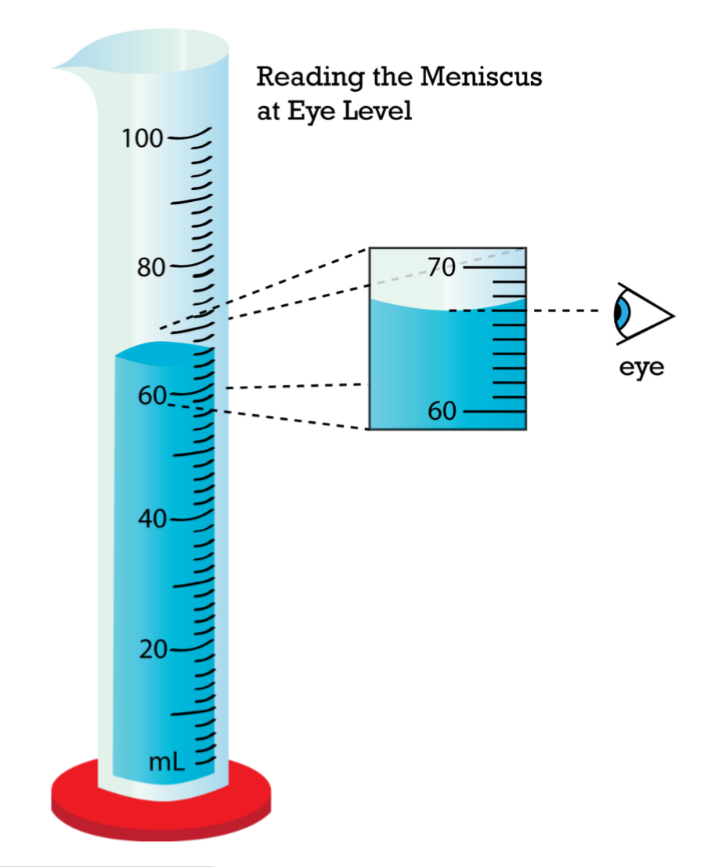
(2) Liquid: use a measuring cylinder
- Pour the liquid into the cylinder
- Read the volume from the scale
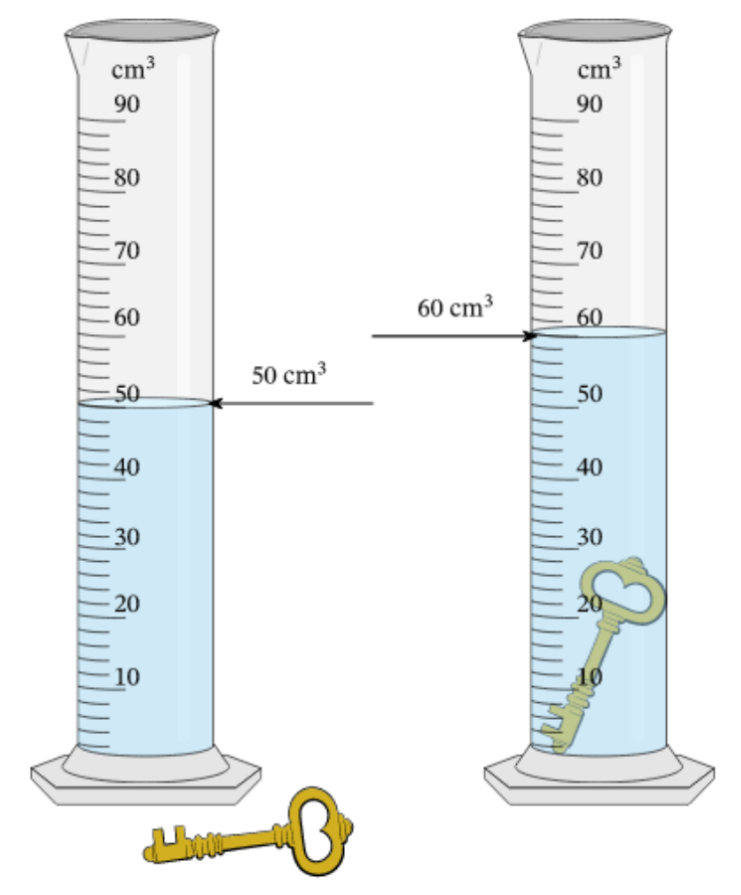
(3) Irregular shape: increased volume
- Submerge the object in water in a measuring cylinder
- Calculate the increase in volume
When unmixable liquids are put together,
- Something sink: they are more dense than water.
- Something float: they are less dense than water.
* Alcohol < Oil < Water (density)
To see which liquid is denser,
- Put those liquid together and see which will stay on top (no need to know their volume or mass)
- But those liquids must be unmixable
* Alcohol < Oil < Water (density)
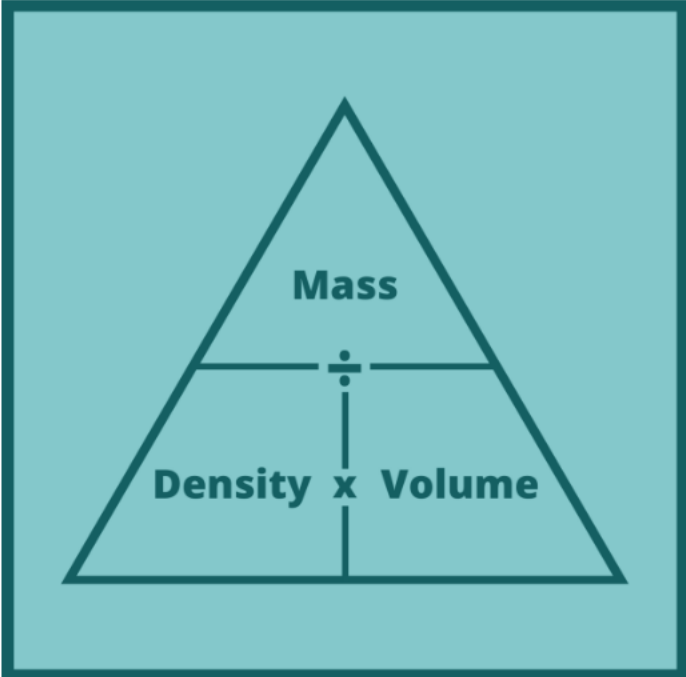
Density = Mass/Volume
ρ (rho/density symbol) = D = m/V
Calculating mass
Mass = Density * Volume
m = D × V
Calculating volume
Volume = mass/density
V = m/D
Density of
Air = 0.0013 cm3
Ice = 0.92 g/cm3
Water = 1 g/cm3
Brick = 2.3 g/cm3
Aluminium = 2.7 g/cm3
Mercury = 13.6 g/cm3
Gold = 19.3 g/cm3

Helium balloon floats in the air.
- Cause the density of helium gas inside it is less than the density of the air outside.
- Heat makes air particles inside move faster (kinetic energy)
- When the gas expands, volume increase whereas mass stays the same.
- D ∝ 1/V (Desnity of the air inside the balloon decrease)
- Desnity of the air inside the balloon < Desnity of the air outside
- That’s why it can float in the air.
The force acting per unit on a surface
If same force, pressure is inversely proportional to surface area.
If same surface area, pressure is directly proportional to force applied.
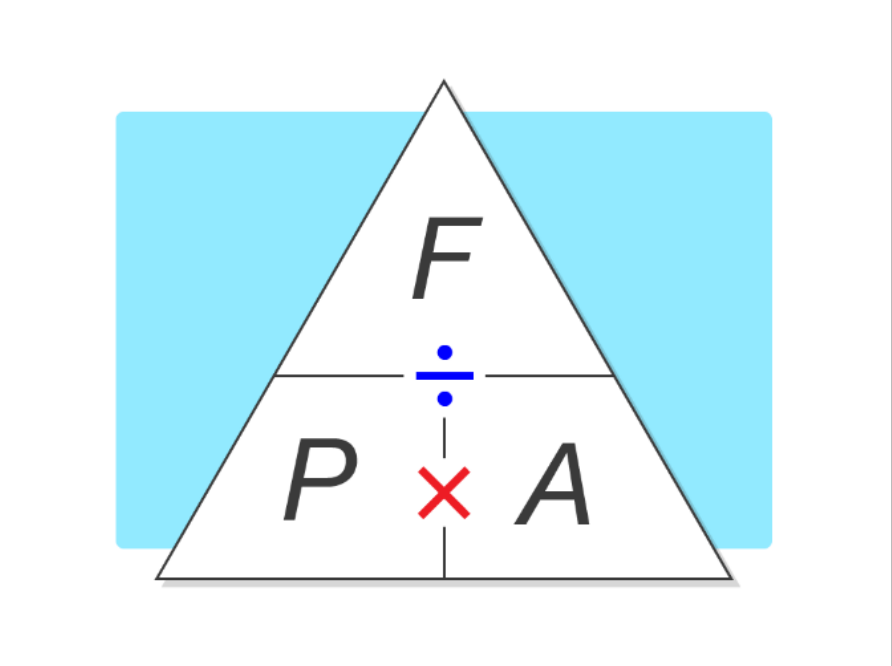
Pressure = force / areae
(P = F / A)
Calculating force
Force = pressure × area
F = P × A
Calculating area
Area = force / pressure
A = F / P
Unit of
- Force - Newton (N)
- Area - cm2, m2, km2, in2, …
- Pressure - N/m2(Newton per meter square) / Pa (Pascal)
1 Pa = 1 N/m2
Atmospheric pressure
- Force applied on a surface by the air above an object
1 atm = 1.01 × 10^5 Pa = 101000 Pa
If objects are under the same pressure,
force affecting on them is directly proportional to their surface area.
| Strenth | Length | Mass | Time | Force |
|---|---|---|---|---|
| F.P.S | foot | pound | second | pound |
| C.G.S | centimeter | gram | second | dyne |
| M.K.S | meter | kilometer | second | newton |
1 kg = 1000 g (g → kg)
1 g = 1/1000 kg
1 g = 1/10^3 kg
1 g = 1 × 10^-3 kg
g/cm3 → kg/m3
1 g/cm3 = 1 g/(1cm×1cm×1cm)
1 g/cm3
= 1 × 10-3 kg / (1 × 10-2)3 m3
= 10-3 kg / 10-6 m3
= 10-3 × 106 kg/m3
= 103 kg/m3
1 g/m3 = 1000 kg/m3
1 m = 100 cm (cm → m)
1 cm = 1/100 m
1 g = 1/10^2 kg
1 g = 1 × 10^-2 kg
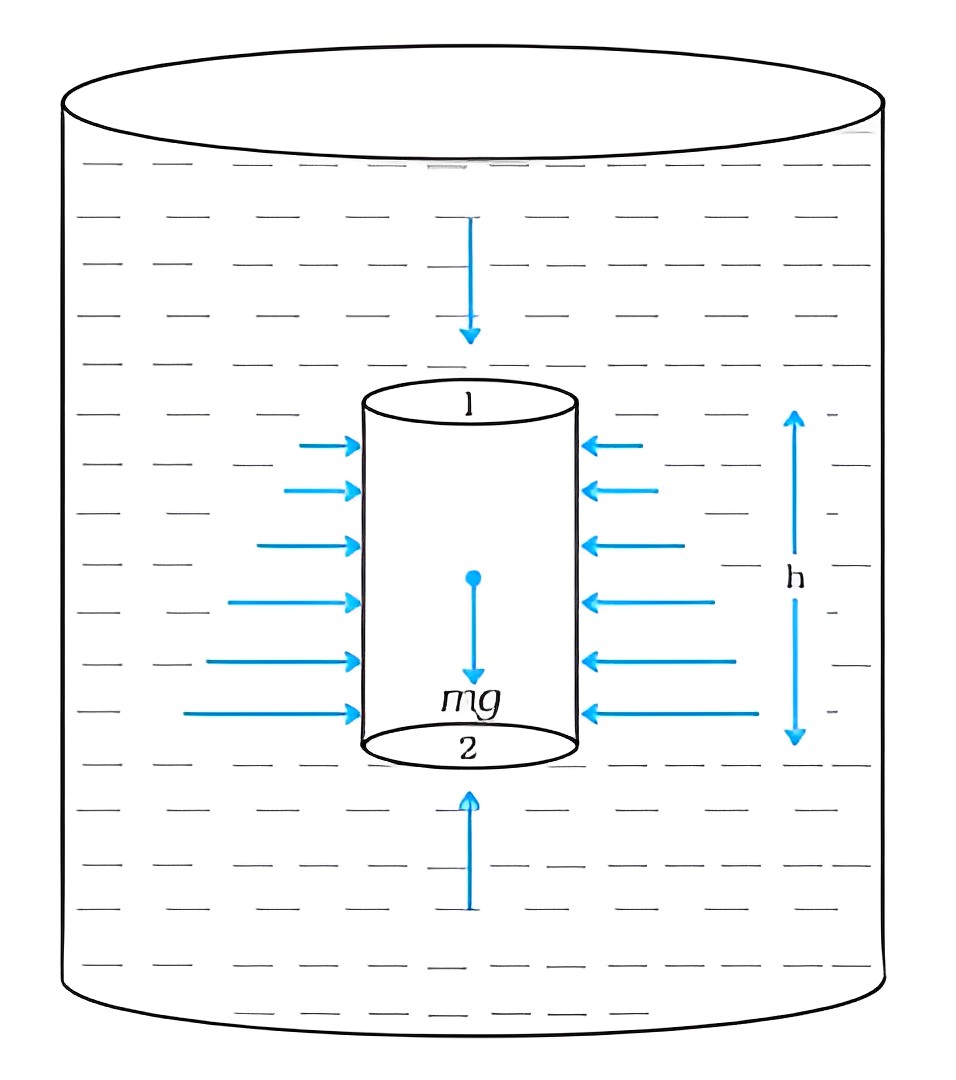
P = F / A
(F = mass/m × accleration due to gravity/g)
P = mg / A
(m = gravity/ρ × V)
P = ρVg / A
(V = area/A × height/h)
P = ρAhg / A
P(liquid) = ρhg (density × height × acceleration due to gravity)
Static fluid pressure does not depend on the shape, total mass or surface area of the liquid.
Solid has greater density than liquid or gas.
Solid → liquid
- volume increase a bit
- mass stays the same
- density decreases
Liquid expands when temperature increases.
Temperature decreases,
- Volume decreases. - Density increases.
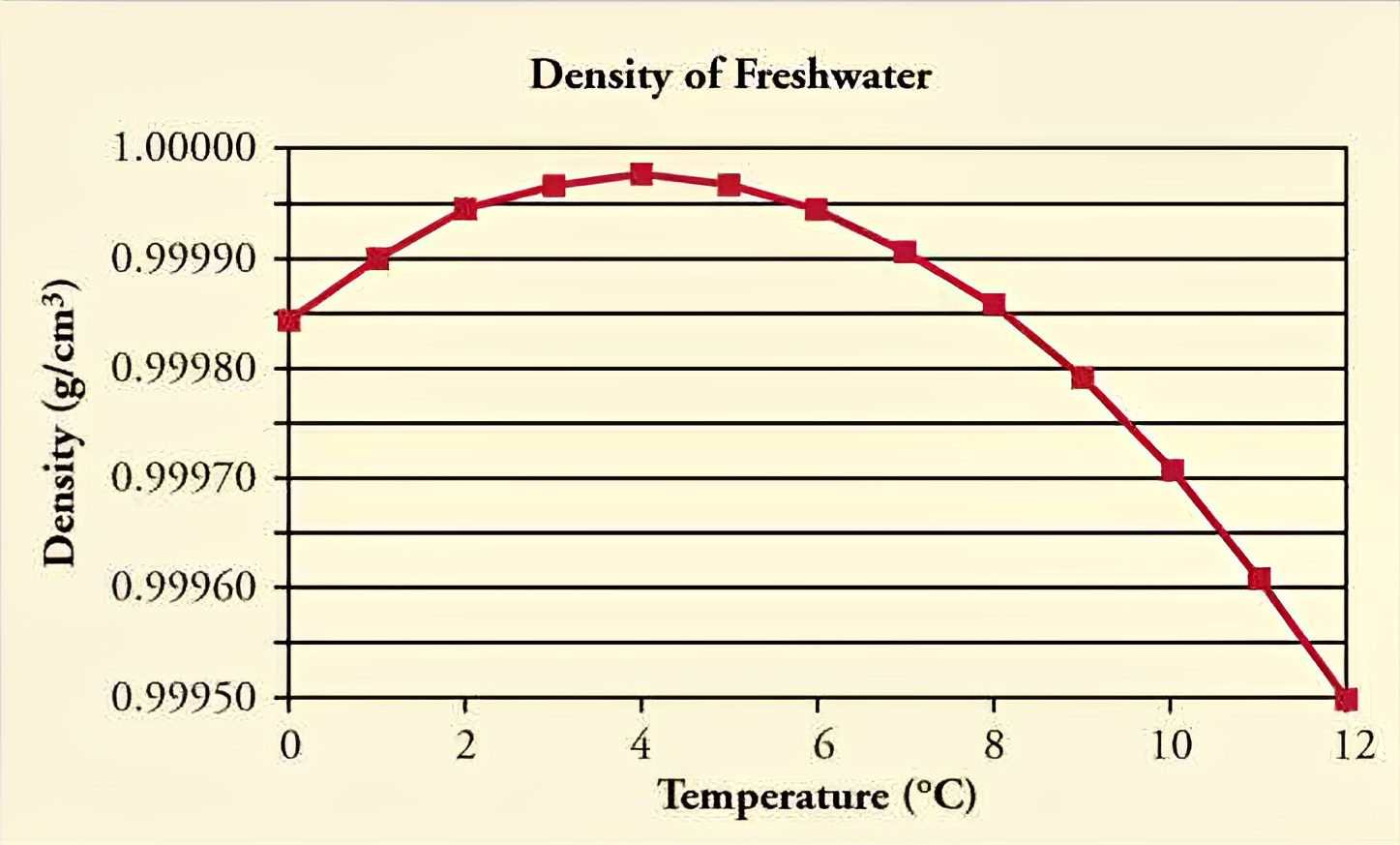
- The maximum density of water is at 4°C.
- Water expands instead of contracting when the temperature goes from 4°C and below.
- The more temperature decreases below 4°C, the more water expands which means its volume increases which make its density decreases as well.
- That’s why ice is less dense than water.
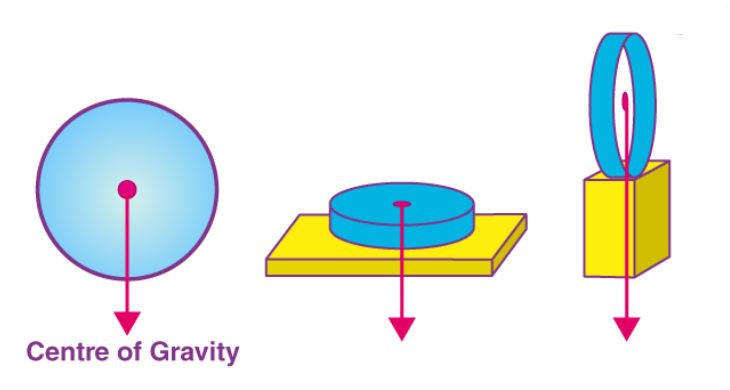
- Quality that has direction - vector quantity
(density, force, pressure)
- Quantity that does not have direction - scalar quantity
(mass, length, energy)
- Quality that has direction - vector quantity
(density, force, pressure)
- Quantity that does not have direction - scalar quantity
(mass, length, energy)
- Quality that has direction - vector quantity
(density, force, pressure)
- Quantity that does not have direction - scalar quantity
(mass, length, energy)
Moment - a measure of the turning effect of a force
For a beam to be balanced,
Clockwise moment = anticlockwise moment

If forces applied are the same, distances from the pivot are the same.
If forces applied have different masses, distances from the pivot are opposite to each other.
(greater mass - nearer to the pivot)
(smaller mass - further form the pivot)
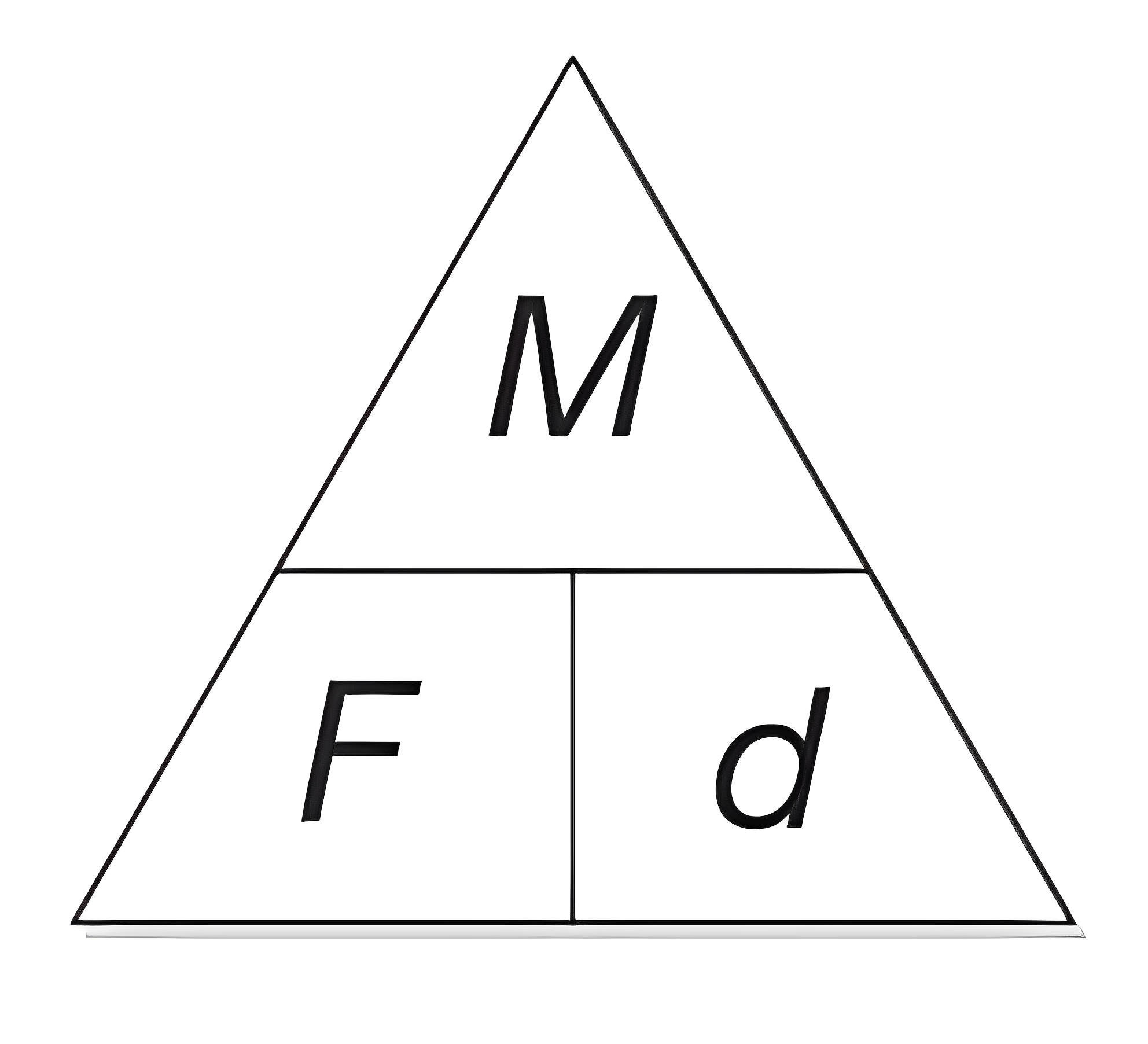
Moment = force × distance from the pivot
(M = F × d)
Calculating force
Force = moment / distance from the pivot
F = M / d
Calculating distance
Distance = moment × force
d = M × F
If forces applied are the same,
Moment ∝ distance from the pivot
If distances from the pivot are the same,
Moment ∝ force applied
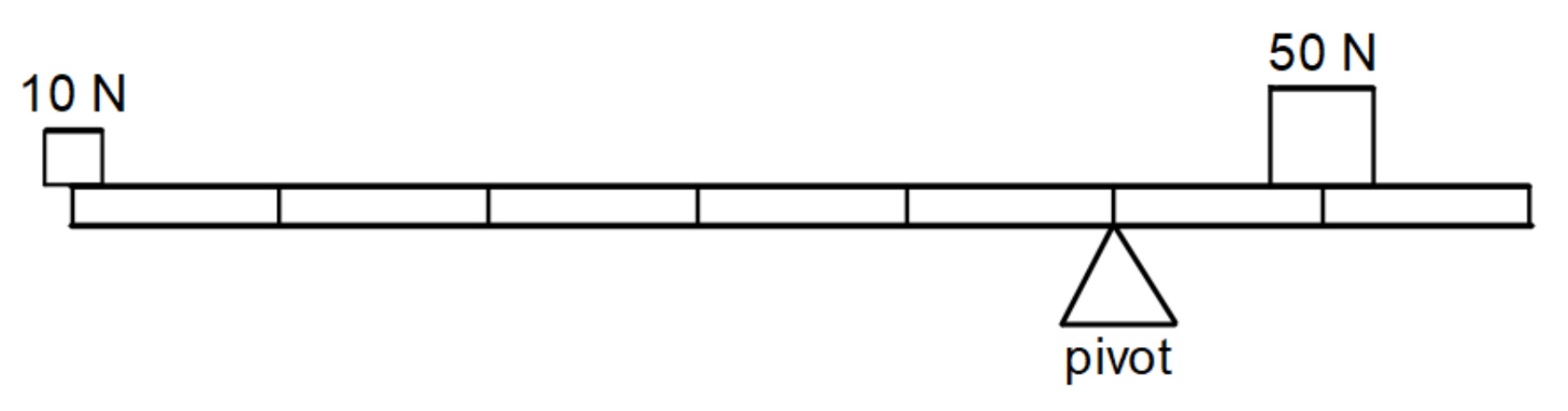
Force = 1(10N) : 5(50N)
Distance = 1(50N) : 5(10N)
Clockwise = 50N × 1 = 50
Anticlockwise = 10N × 5 = 50
Moments are equal and they’re balanced.